Dice in HGB 3.0
First off, thank you to Nick (prof9844) for all his hard work in generating the raw data used in this post. First off, let’s describe the overall dice mechanism.
- Every roll starts with 2d6, and is against the relevant stat, which ranges from 2+ to 6+.
- You may add or subtract 1d6 based on various modifiers or criteria, but you never decrease your dice pool below 1d6.
- You calculate your final “Roll Result” as follows:
- Pick the die that has rolled the highest number, and set it aside. That is your initial result.
- For every other die (including ties for the highest number) that meets or exceeds the relevant stat, you get a “success.”
- Add 1 to your initial result for every success to determine your roll result.
Here are some examples:
| Die Pool | Stat | Rolls | Roll Result |
|---|---|---|---|
| 2d6 | 4+ | 1,1 | 1 |
| 2d6 | 4+ | 4,4 |
5 |
| 3d6 | 5+ | 4,5,6 | 7 |
| 3d6 | 3+ | 1,1,2 | 2 |
| 3d6 | 4+ | 4,4,5 |
7 |
Most rolls in Heavy Gear Blitz are opposed. In other words, the attacking player and the defending player both calculate your dice pool, roll, and each come up with your roll result independently. You then subtract the defender’s result from the attacker’s result to determine the “Margin of Success” or MoS. The MoS will determine (along with weapon and armor values) the amount of damage the defender takes. A negative MoS is a failure.
That’s a lot of confusing stuff, so basically the idea is you want to roll a pile of d6. You want to roll a bigger number than your opponent’s number so your MoS is the biggest! So, what do the average die rolls (not MoS) look like?

Oh god, that’s just a pile of numbers! Well yes. Here are some obvious takeaways:
- You want to have more dice than your opponent.
- You want to have a lower skill than your opponent.
Some less obvious takeaways is that it’s better to increase the number of dice if you have a good skill, and better to improve your skill (if it’s high) if you have a lot of dice. For example, going from 1d6 to 2d6 at skill 3+ is a 1.42 bump on average, whereas going from a 3+ to 2+ skill on 2d6 is only a 0.25 improvement.
On the other hand, going from 5d6 to 6d6 at skill 6+ is a measly 0.22 improvement, whereas going from 6+ to 5+ on 6d6 is a much more attractive 0.76 improvement. It’s worth nothing that it’s quite difficult to improve your skill during the game. There are a number of improvements you can make at the time you construct your list, but very few ways you get improve your skill when you hit the table. This makes this part of the discussion a bit of a moot point, but it’s interesting nonetheless. So, more dice, more better?
Well, it can be often pretty taxing on your in game resources to generate more dice — you may have to expose some of your units to return fire to get some bonus dice or a skill bonus, or you may have to have paid to take a bigger, better guy with better rules. So the question is, what is the “right amount of dice” to roll, or perhaps rephrased, what is the right amount of effort to expend to get dice?
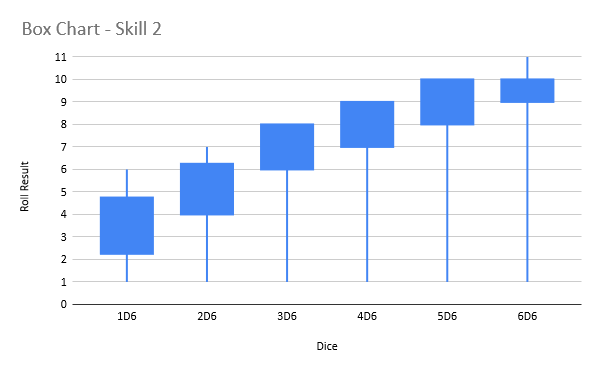
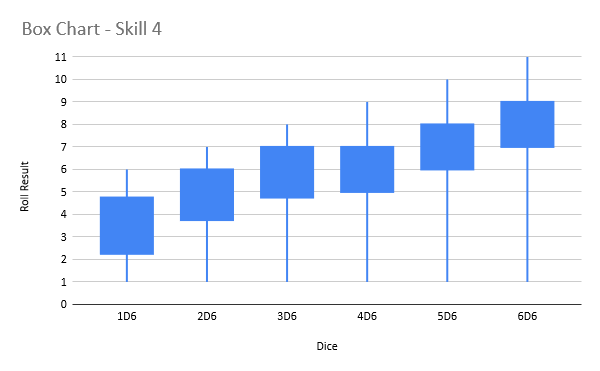
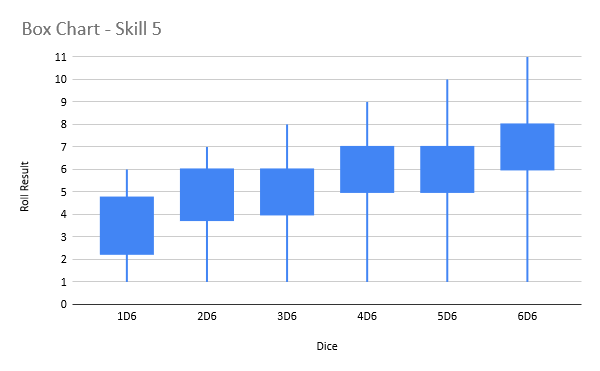
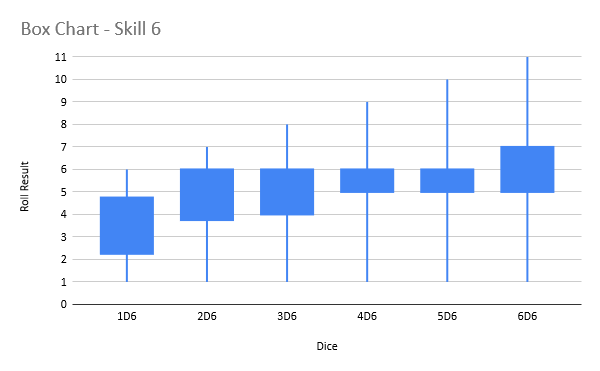
For that, we can turn to some box plots. Basically the lines show the maximum and minimum possible Roll Result, and the box shows the range 50% of your possible rolls will fall into, with 25% below the box and 25% above the box.
What this tells us is that
- 2d6 is definitely better than 1d6.
- 3d6 is good enough for the most common skill value of 4+. There isn’t much incentive to get to 4d6 or higher unless you have a skill of 3+ or 2+.
Also it’s worth noting that there are ways to just straight up get a +1 to your Roll Result, like the Precise and Advanced rules, which are very good for high (bad) skill units. This often is much better than getting +1d6, especially once you get to 4d6 and above for high skill models (4+, 5+, 6+).
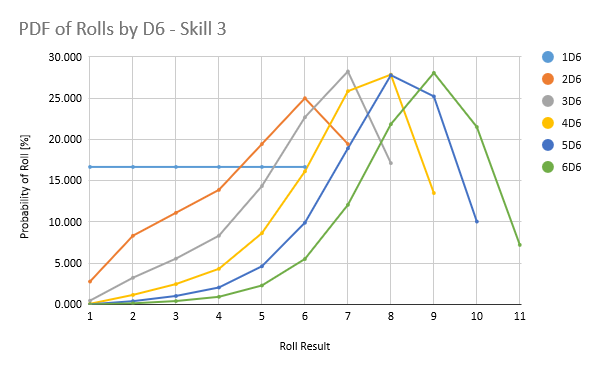
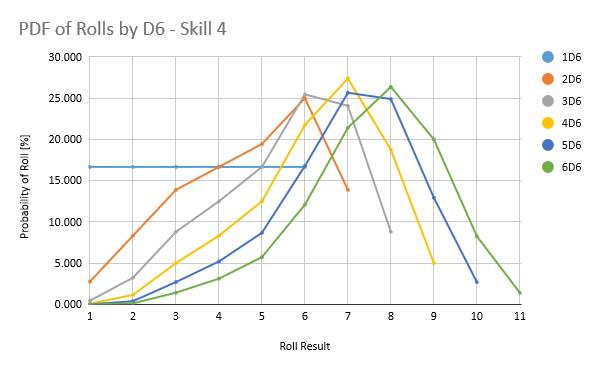
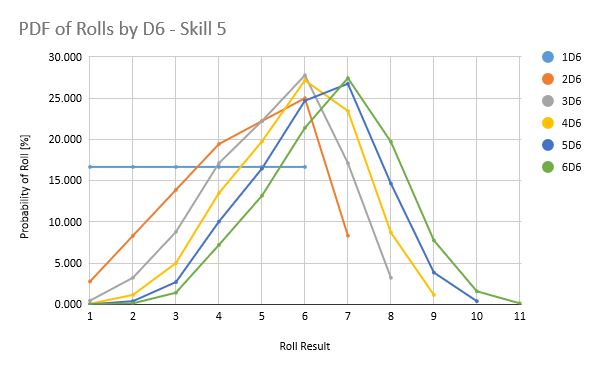
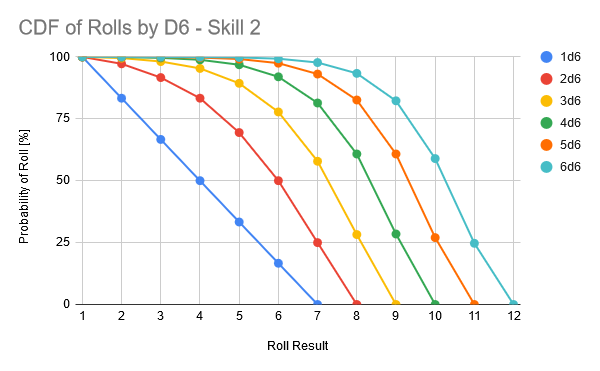
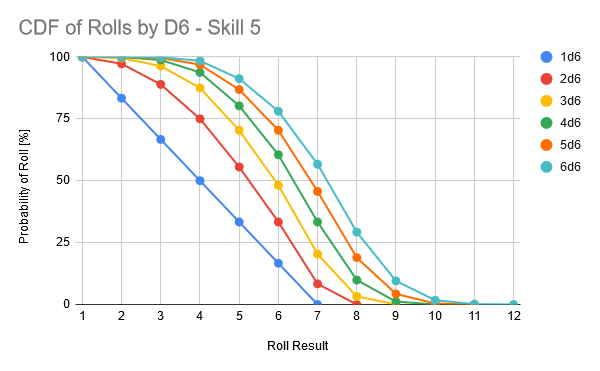
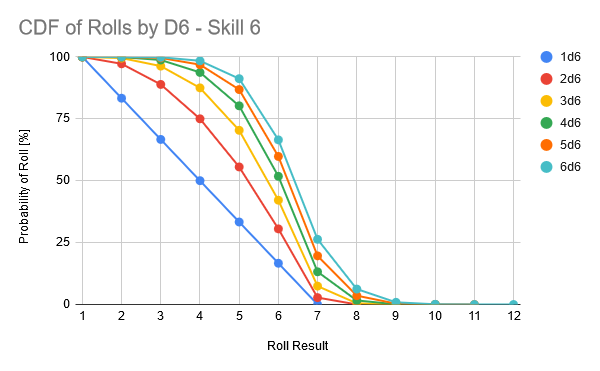
If you’re a statistics person, you can have a look at the PDF and CDF plots below:
CDF
And that’s that!